다이나믹 프로그래밍(동적 계획법)
개념
- 한 번 계산한 문제는 다시 계산하지 않도록 하는 알고리즘
- 연산속도와 메모리 공간을 최대한으로 활용할 수 있는 효율적인 알고리즘
- 큰 문제를 작게 나누고, 같은 문제라면 한 번씩만 풀어 문제를 효율적으로 해결한다.
- 다이나믹 프로그래밍 vs 분할정복(ex. 퀵 정렬)
동적 계획법의 접근 방식은 기본적으로 분할 정복 알고리즘과 비슷하다. 위에서도 설명했지만 동적 계획법을 사용하는 알고리즘 역시 주어진 문제를 부분 문제로 나누어 각 부분 문제의 답을 계산하고, 이 계산한 결과값을 이용해 원래 문제의 답을 산출하기 때문이다. 여기서 분할정복과 차이가 생기는 부분은 원래의 문제를 부분 문제로 나누는 방식에 있다. 동적 계획법의 경우 주어진 문제를 나눌 때 부분 문제를 최대한 많이 이용하도록 나눈 다음, 주어진 부분 문제의 정답을 한 번만 계산하고 저장해둔 뒤 다시 한 번 이 부분 문제를 이용할 때에는 저장해둔 정답을 바로 산출하여 이용함으로써 속도를 향상시킨다.
사용 조건
1) 큰 문제를 작은 문제로 나눌 수 있다.
2) 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.
구현 방식
1) 탑다운 방식(하향식) : 메모이제이션은 탑다운 방식에 국한되어 사용되는 표현이다.
2) 보텀업 방식(상향식) : 다이나믹 프로그래밍의 전형적인 형태. 이 방식에서 사용되는 결과 저장용 리스트 = DP 테이블 이다.
3) 메모이제이션 기법(캐싱) : 한 번 구한 결과를 메모리 공간에 메모해두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법 :파이썬에서는 이미 구한 정답을 리스트에서 가져오면 된다. dict 자료형 또한 이용 가능하다. 사전 자료형은 연속적이지 않은 데이터 특성인 경우에 유용하다. n 번째 수를 구하고자 할 때, 0부터 n-1 모두가 아닌 일부의 작은 문제에 대한 해답만 필요할 경우 사용하면 효과적이다.
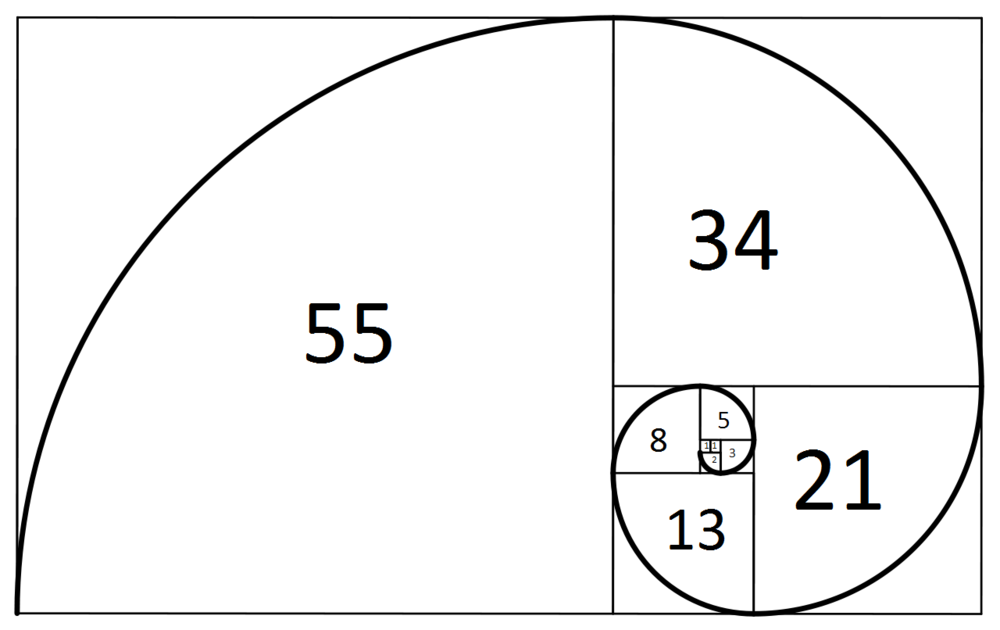
피보나치 수를 구하는 과정에서의 동적 계획법
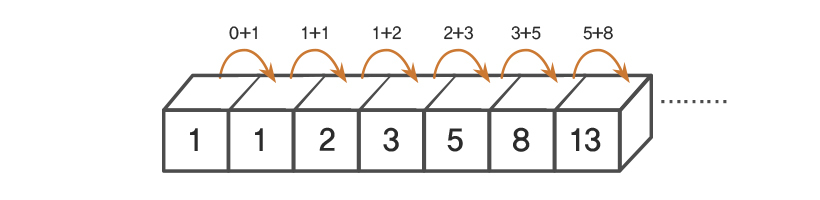
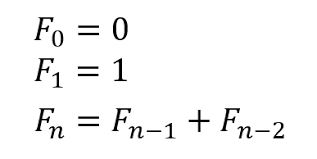
파이썬으로 연속된 많은 데이터 수열을 리스트로 처리할 수 있다. 수학적 점화식은 재귀 함수를 사용하면 간단하지만 N이 커질 수록 수행 시간이 기하급수적으로 늘어나는 문제가 있다. 이러한 경우 다이나믹 프로그래밍을 사용하면 효율적으로 해결할 수 있다.
# 재귀 방식
# 한 번 계산된 결과를 메모이제이션하기 위한 리스트 초기화
d = [0] * 100
# 피보나치 함수를 재귀함수로 구현 (탑다운 다이나믹 프로그래밍)
def fibo(x):
print('f(' + str(x) + ')', end=' ') # 호출되는 함수
if x == 1 or x == 2: # 종료 조건
return 1
if d[x] != 0: # 이미 계산한 적 있는 문제라면 그대로 반환
return d[x]
# 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
d[x] = fibo(x-1) + fibo(x-2)
return d[x]
print(fibo(99))
# 출력 결과 :
'''
f(99) f(98) f(97) f(96) f(95) f(94) f(93) f(92) f(91) f(90) f(89) f(88) f(87) f(86) f(85) f(84) f(83) f(82) f(81) f(80) f(79) f(78) f(77) f(76) f(75) f(74) f(73) f(72) f(71) f(70) f(69) f(68) f(67) f(66) f(65) f(64) f(63) f(62) f(61) f(60) f(59) f(58) f(57) f(56) f(55) f(54) f(53) f(52) f(51) f(50) f(49) f(48) f(47) f(46) f(45) f(44) f(43) f(42) f(41) f(40) f(39) f(38) f(37) f(36) f(35) f(34) f(33) f(32) f(31) f(30) f(29) f(28) f(27) f(26) f(25) f(24) f(23) f(22) f(21) f(20) f(19) f(18) f(17) f(16) f(15) f(14) f(13) f(12) f(11) f(10) f(9) f(8) f(7) f(6) f(5) f(4) f(3) f(2) f(1) f(2) f(3) f(4) f(5) f(6) f(7) f(8) f(9) f(10) f(11) f(12) f(13) f(14) f(15) f(16) f(17) f(18) f(19) f(20) f(21) f(22) f(23) f(24) f(25) f(26) f(27) f(28) f(29) f(30) f(31) f(32) f(33) f(34) f(35) f(36) f(37) f(38) f(39) f(40) f(41) f(42) f(43) f(44) f(45) f(46) f(47) f(48) f(49) f(50) f(51) f(52) f(53) f(54) f(55) f(56) f(57) f(58) f(59) f(60) f(61) f(62) f(63) f(64) f(65) f(66) f(67) f(68) f(69) f(70) f(71) f(72) f(73) f(74) f(75) f(76) f(77) f(78) f(79) f(80) f(81) f(82) f(83) f(84) f(85) f(86) f(87) f(88) f(89) f(90) f(91) f(92) f(93) f(94) f(95) f(96) f(97) 218922995834555169026
'''재귀 함수를 사용하면 컴퓨터 시스템에서는 함수를 다시 호출했을 때 메모리 상에 적재되는 일련의 과정 때문에 오버헤드가 발생할 수 있다. 따라서 반복문을 사용하여 오버헤드를 줄일 수 있다. (성능 up)
# 반복문 방식
d = [0] * 100
d[1] = 1
d[2] = 1
n = 99
for i in range(3, n + 1):
d[i] = d[i - 1] + d[i - 2]
print(d[n])
문제 풀이 팁
- 완전탐색으로 접근했을 때 시간이 매우 오래 걸리면 다이나믹 프로그래밍을 적용할 수 있는지 사용 조건을 체크한다.
- 메모이제이션을 활용하여 코드를 개선할 수 있다.
- 재귀 함수 사용하는 탑다운 방식보다는 보텀업 방식으로 구현하는 것을 권장한다.(재귀 함수 스택 한정 이유)
- 피보나치 수열 구현 방식을 연습해두자.
- 3차원 리스트를 이용해야 하는 문제는 최단 경로의 플로이드 워셜 알고리즘을 이용하여 시도가 필요하다.
'Algorithm > Study' 카테고리의 다른 글
| 최단 경로 알고리즘 : 플로이드 워셜 (0) | 2021.09.24 |
|---|---|
| 최단 경로 알고리즘 : 다익스트라 (0) | 2021.09.24 |
| 이진탐색 알고리즘 (Python) (0) | 2021.09.24 |
| 그래프 탐색 알고리즘 : BFS (Python) (0) | 2021.09.17 |
| 그래프 탐색 알고리즘 : DFS (Python) (0) | 2021.09.17 |



